

This is not quite right, but then we "know" (as in, we've exposed ourselves to this a billion times already) that $16 = 4^2$, so this is in fact $1+(x/4)^2$.
#U sub integration how to
Again, multiplying or dividing by constants isn't an issue because if we know how to integrate $f$ we know how to integrate $16 \cdot f$. One could try to first get rid of that $16$.

So essentially we would like to transform $16+x^2$ into something of the sort of $1+u^2$.
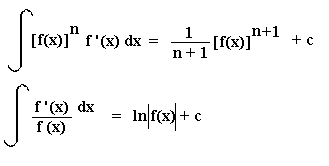
Note that the $4$ in the numerator isn't really an issue, you can take that "outside the integral", informally speaking. That's how you just "know" $\mathbf$ is involved ( edit: OP said so in the original version post). For most of us which haven't been integrating since kindergarten, a way to "see it" is to do plenty of exercises. This product is protected by copyright and distributed under licenses restricting its use, copying, distribution, and decompilation.Unfortunately for everyone there's no general way of doing this. © Maplesoft, a division of Waterloo Maple Inc., 2023. Prove that ∫ − a a f x &DifferentialD x = 2 ∫ 0 a f x &DifferentialD x for any even function f. Prove that ∫ − a a f x &DifferentialD x = 0 for any odd function f. Verify that ∫ − &pi &pi sin x &DifferentialD x = 0, and that ∫ − &pi / 2 &pi / 2 cos x &DifferentialD x = 2 ∫ 0 &pi / 2 cos x &DifferentialD x. Įvaluate the definite integral ∫ 2 3 x 3 x 2 + 3 &DifferentialD x. Įvaluate the indefinite integral ∫ x 3 x 2 + 3 &DifferentialD x. Įvaluate the indefinite integral ∫ x 1 − 3 x 2 &DifferentialD x. Įvaluate the indefinite integral ∫ 2 x + 1 8 &DifferentialD x. For the even function, the yellow and red regions match exactly, but for the odd function, the yellow and red regions match in magnitude, but differ in sign.Įvaluate the indefinite integral ∫ 3 x − 2 &DifferentialD x. In each case, the region shaded in yellow to the left of the y -axis represents the value of the definite integral on − a, 0 the region shaded in red to the right of the y -axis, the value of the definite integral on 0, a. Table 4.4.2 Definite integral of an odd or even function over a symmetric interval Table 4.4.2 details the value of a definite integral of an odd or even function taken over a symmetric interval such as − a, a. No matter how the substitution rule is given, an explicit solution for y = y x is needed for expressing the indefinite integral in terms of x. In either of these cases, obtain dx by solving explicitly for x and differentiating, or by differentiating implicitly. Īlternate forms for the substitution are y = h x and r y = s x. If F y is the antiderivative obtained when the substitution x = g y is made in the indefinite integral, then F g − 1 x is an indefinite integral in terms of the original variable, x correspondingly, the value of the definite integral is given by F g − 1 b − F g − 1 a = F g − 1 x &verbar a b. Table 4.4.1 Substitution in definite and indefinite integrals ∫ a b f x &DifferentialD x = ∫ g − 1 a g − 1 b f g y &DifferentialD y ∫ f x &DifferentialD x = ∫ f g y g ′ y &DifferentialD y = F y = F g − 1 x Table 4.4.1 lists the rule for making a substitution, or change of variable, in an integral.


 0 kommentar(er)
0 kommentar(er)
